Improper integrals are useful for solving a variety of problems. A horizontally infinite improper integral contains either ∞ or –∞ (or both) as a limit of integration.
Evaluating an improper integral is a three-step process:
A horizontal improper integral occurs when a definite integral has a limit of integration that’s either ∞ or –∞. This type of improper integral is easy to spot because infinity is right there in the integral itself. You can’t miss it.
For example, suppose that you want to evaluate the following improper integral:
Here’s how you do it, step by step:
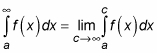
Before moving on, reflect for one moment that the area under an infinitely long curve is actually finite. Ah, the magic and power of calculus!
Similarly, suppose that you want to evaluate the following:
Here’s how you do it:
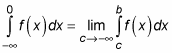
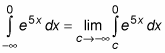Expressing the integral as the limit of a proper integral." width="165" height="53" />
Again, calculus tells you that, in this case, the area under an infinitely long curve is finite.
Of course, sometimes the area under an infinitely long curve is infinite. In these cases, the improper integral can’t be evaluated because the limit does not exist (DNE). Here’s a quick example that illustrates this situation:
It may not be obvious that this improper integral represents an infinitely large area. After all, the value of the function approaches 0 as x increases. But watch how this evaluation plays out:
At this point, you can see that the limit explodes to infinity, so it doesn’t exist. Therefore, the improper integral can’t be evaluated, because the area that it represents is infinite.
Mark Zegarelli, a math tutor and writer with 25 years of professional experience, delights in making technical information crystal clear — and fun — for average readers. He is the author of Logic For Dummies and Basic Math & Pre-Algebra For Dummies.
